扇形面积公式3个,扇形的周长和面积公式
本文目录
1.扇形的周长和面积公式 2.扇形的面积公式是什么 3.扇形的周长和面积公式 4.扇形面积公式是什么
扇形的周长和面积公式
扇形面积公式:S扇形=nπR/360=LR/2.R是扇形半径,n是弧所对圆心角度数,π是圆周率,也可以用扇形所在圆的面积除以360再乘以扇形圆心角的角度n。

扇形面积公式具体算法:
弧长公式:n是圆心角度数,r是半径,α是圆心角弧度。
l=nπr÷180或l=n/180·πr或l=|α|r。
在半径是R的圆中,因为360°的圆心角所对的弧长就等于圆周长C=2πR,所以n°圆心角所对的弧长为l=n°πR÷180°。
在弧度制下,若弧所对的圆心角为θ,则有公式L=Rθ。
扇形面积公式S=LR/2,相对应的则有扇形面积计算公式S=RRθ/2。
S扇 = L R / 2 (L为扇形弧长,R为半径)或π(R^2)*N/360(即扇形的度数)。
扇形是与圆形有关的一种重要图形,其面积与圆心角(顶角)、圆半径相关,圆心角为n°,半径为r的扇形面积为n/360*πr^2。如果其顶角采用弧度单位,则可简化为1/2×弧长×(半径)。
扇形的面积公式是什么
1、扇形的面积已知圆心角:
其中弧度制为:
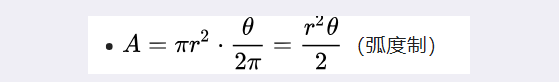
其中π是圆周率,r是底圆的半径,θ是圆心角的弧度数。
角度制为:

其中π是圆周率,r是底圆的半径,n是圆心角的度数。
2、扇形的面积已知弧长:
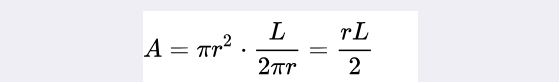
其中π是圆周率,r是底圆的半径,L是弧长。
3、扇形面积的积分形式:
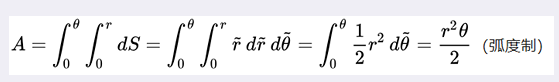
其中r是底圆的半径,θ是圆心角的弧度数。
扩展资料:
扇形面积的推导。扇形是从圆形钟剪切下来一部分,圆的面积公式:πr²,表示的是360度的圆心角所对应的弧长,假设一个扇形的圆心角为n度。360度的圆形面积是πr²,则1度为πr²/360,n度就是nπr²/360。这样S(扇形)=nπr²/360。
再来,扇形弧长的推导。360度的圆的弧长为:2πr,1度的弧长为:πr/180。n度则为:nπr/180。换算成弧长:nπr/π=nr;即l=nr;
前面得到扇形的面积:S(扇形)=nπr²/2π=nr*r/2=1/2*l*r,哈哈是不是很简单,扇形公式就这样推导出来了。
参考资料来源:百度百科——扇形
扇形的周长和面积公式
扇形周长公式为:扇形周长=扇形半径×2+弧长,即C=2r+ (n÷360) πd=2r+(n÷180)πr。扇形面积公式是S=(lR)/2或S=(1/2)θR²,R是底圆的半径,l为扇形弧长,θ为圆心角。

一条圆弧和经过这条圆弧两端的两条半径所围成的图形叫扇形(半圆与直径的组合也是扇形)。扇形周长公式是:扇形周长=扇形半径×2+弧长,即C=2r+ (n÷360)πd=2r+(n÷180)πr。扇形面积公式描述了扇形面积和圆心角(顶角)、半径、所对弧长的关系。数学公式表示为:S扇=(lR)/2 (l为扇形弧长) =(1/2)θR²(θ为以弧度表示的圆心角)。

扇形(符号:⌔),是圆的一部分,由两个半径和和一段弧围成,在较小的区域被称为小扇形,较大的区域被称为大扇形。θ是扇形的角弧度,r是圆的半径,L是小扇形的弧长。圆弧为180°的扇形称为半圆。其他圆弧角的扇形有时给予其特别的名字,其中包括象限角(90°)、六分角(60°)以及八分角(45°),它们分别是整圆的1/4、1/6、1/8。

扇形的组成部分:
1、圆上A、B两点之间的的部分叫做“圆弧”简称“弧”,读作“圆弧AB”或“弧AB”。
2、以圆心为中心点的角叫做“圆心角”。
3、有一种统计图就是“扇形统计图"。
扇形面积公式是什么
扇形面积公式是:S=LR/2
公式说明:S是面积,L为扇形弧长,R为半径,α为弧度制下的扇形圆心角。
若命扇形的顶角(扇形的弧所对的圆心角,叫做扇形的顶角)为a,那么:
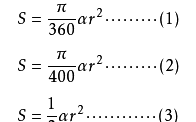
其中
(1)式适用于六十分制。
(2)式适用于百分制。
(3)式适用于径制(弧度制)。
扩展资料:
扇形是与圆形有关的一种重要图形,其面积与圆心角(顶角)、圆半径相关,圆心角为n°,半径为r的扇形面积为n/360*πr^2。如果其顶角采用弧度单位,则可简化为1/2×弧长×(半径)
扇形还与三角形有相似之处,上述简化的面积公式亦可看成:1/2×弧长×(半径),与三角形面积:1/2×底×高相似。
弧长(L)=n/360·2πr=nπr/180,扇形的弧相似三角形的一条边。
应用实例如下:
如图,边长为1试题的菱形ABCD绕点A旋转,作AM垂直于BC,连接AC。当B,C两点恰好落在扇形AEF的弧EF上时,求弧BC的长
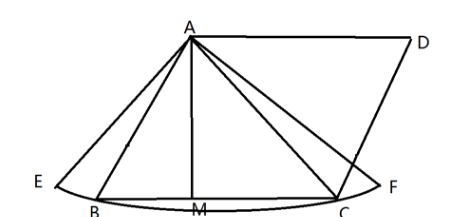
解:
菱形ABCD,AB=BC=1,∠BAC=∠BCA
当B,C两点恰好落在扇形AEF的弧EF上时,AB=AC=AE=AF=1,∠CBA=∠BCA
所以,∠BAC=∠BCA=∠CBA=60°
弧BC的长:60°=2π*AE:360°
弧BC的长=2π*1/6=π/3.
以上就是关于扇形面积公式3个,扇形的周长和面积公式的全部内容,以及扇形面积公式的相关内容,希望能够帮到您。