年金现值公式推算过程(年金终值、年金现值公式的推导过程)
年金终值(F/A,i,n)、(A/F,i,n),年金现值(P/A,i,n)、(A/P,i,n)作为资金时间价值计算必备的知识点,是财务及经济考试的必考点,几乎涵盖了所有的职业资格考试,就我所知道的会计师、造价师、建造师、监理师、咨询师、勘察设计类等都会涉及,可以说是非常非常重要的一个知识点了。而年金终值、年金现值相对来说可以算是一个比较难的知识点,特别是公式比较复杂,容易记混。我以前都是强行记忆,感觉效果并不是很好,往往需要现场进行试验才行。最近在备考咨询师的过程中,老师对公式的推导过程进行了讲解,让我觉得理解更深了一步,所以第一时间和大家进行分享,便于大家在理解的基础上进行记忆,这样效果更好。当然肯定有很多朋友对这个掌握得比我好多了,若有说得不对的地方还请批评指正,不要笑话就好。
一、例子:
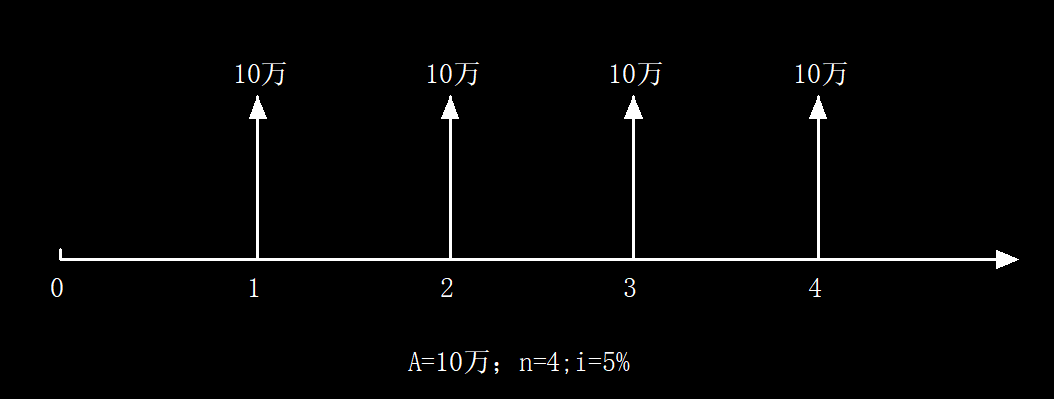
现金流量图
以图示现金流量图为例,每期存入银行A=10万元,利率i=5%,到第四期末本利和F为多少?
二、 年金终值(F/A,i,n)推导过程:
1、以复利的方式计算,这一步过程是推导的基础,年金终值公式正是在这个基础上化解出来的:
F=A*(1+i)^3+A*(1+i)^2+A*(1+i)^1+A=A*【(1+i)^3+(1+i)^2+(1+i)^1+1】
=10*【(1+5%)^3+(1+5%)^2+(1+5%)^1+1】
2、【(1+i)^3+(1+i)^2+(1+i)^1+1】是一个等比数列,且公比q=(1+i)=(1+5%),所以数列和Sn=(1-q^n)/(1-q),将q替换成(1+i),则Sn=[1-(1+i)^n]/[1-(1+i)]=[(1+i)^n-1]/i
3、结合1和2,则F=A*[(1+i)^n-1]/i=10*[(1+5%)^4-1]/5%,反之A=F* i/[(1+i)^n-1]。

手写版
三、年金现值(P/A,i,n)推导过程
根据F=A*[(1+i)^n-1]/i和F=P(1+i)^n,可知A*[(1+i)^n-1]/i=P(1+i)^n,
所以A=P* i(1+i)^n/[(1+i)^n-1];P=A*[(1+i)^n-1]/i(1+i)^n。

手写版